WRITING SERVICE AT YOUR CONVENIENCE



At Buy Cheap College Essays, we employ a large team of skilled writers. Their rating is based on previous customer reviews and rates. Before you hire a writer, you can familiarize yourself with his track record in detail.











Essay
Business Plan
Presentation or Speech
Admission Essay
Case Study
Reflective Writing
Annotated Bibliography
Creative Writing
Report
Term Paper
Article Review
Critical Thinking / Review
Research Paper
Thesis / Dissertation
Book / Movie Review
Book Reviews
Literature Review
Research Proposal
Editing and proofreading
Other

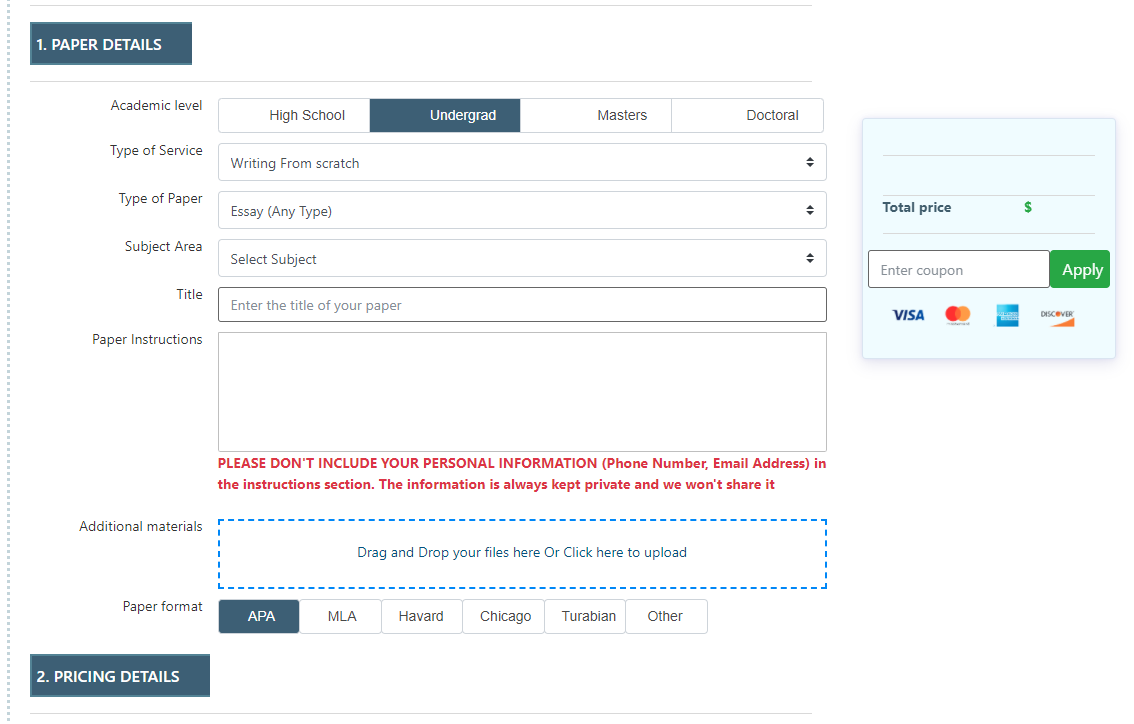
Fill out order details and instructions, then upload any files or additional materials if needed. Then, confirm your order by clicking “Place an Order.”

Read the feedback and look over the ratings to choose the writer that suits you best.

Check the inbox for notifications, download the completed assignment, and then release the payment.





Each writer passes a series of grammar and vocabulary tests before joining our team.
We care about the privacy of our clients and will never share your personal information with any third parties or persons.
A plagiarism report from Turnitin can be attached to your order to ensure your paper's originality.
We process all payments through PCI DSS Level 1 gateways to ensure maximum safety of your data.
Every sweet feature you might think of is already included in the price, so there will be no unpleasant surprises at the checkout.
You can contact us any time of day and night with any questions; we'll always be happy to help you out.

Get all these features for $65.77 FREE
Yes, absolutely! When you make your first sign up, you get a personal cabinet for your comprehensive experience.
You will be able to provide the instructions or attach files directly to the order.
Additionally, you will be able to chat with your essay writer and discuss any specific details or ask any questions.
We guarantee the originality of all our papers and have a zero-tolerance policy towards plagiarism.
We can provide you with a free plagiarism report from Turnitin (upon request).
The minimum deadline is 6 hours, but if your assignment isn’t complicated, we may be able to adjust to your time-frame needs. Simply give us a deadline, and we’ll get it done.
We also offer discounts depending on the urgency of your assignment. The further your deadline, the lower the price per page will be.
A deposit needs to be made so you can reserve a writer. The writer will only receive the money after you receive the final copy, checked it, and made sure that it’s written according to the provided instructions.
Consider it our quality guarantee.
First of all, we will do our best to ensure that everything goes well.
If something needs to be changed/fixed/amended, we will revise your paper an unlimited number of times, free of charge, until you are satisfied with the results.
We also provide 24/7 support to assist you whenever you need it!
You can view the bio of each writer who bids on your order and also see their stats. For example, the number of completed orders, success rate, and the reviews for each and every writer! Plus, you can chat with any of the candidates prior to hiring them.
If you have doubts about who you should hire to complete your “write my essay” request, you can always contact us, and we will find the most suitable writer for your assignment.
We are certified by Visa, Mastercard, American Express, and Discover. Furthermore, we process all payments through PCI DSS Level 1 gateways, which ensures complete security and privacy of your payments.
Sure thing, we do!
When you order essays from our essay writing service, you get the following features for free:
• Plagiarism report
• Unlimited Revisions
• Title Page
• Formatting
• Best writer
• Outline
Want an A to Z guide on how to write an essay? If you’re tired of the boring lectures from your professor, then subscribe to our YouTube channel. Here, we explore everything related to essay writing in a smooth and easy to understand way.
On Instagram, we share the freshest student memes daily! And that’s not all; you can order any paper by simply sending a DM. Be the first one to know about all the EssayPro updates, giveaways, and seasonal discounts for students. Follow our social media accounts to stay updated.
Our essay writing company has been active since 1997. With over 20 years of experience in the custom essay writing industry, we have helped over thousands of students reach their full academic potential. Each essay writer passed our frame selection and fit the qualification requirements of Buy Cheap College Essays.
We offer papers of any kind and academic level: high-school, college, and university. Including case study, research paper, assignments, dissertation, term paper, M/As, and doctorates. Regardless of the subject, we are ready to deliver high-quality custom writing orders to consumers upon their first write my essay for me request.
Every paper is written with the customer’s needs in mind and plagiarism-free under strict quality assurance protocol to bring effective results to consumers. Writer managers at our essay writing service work around the clock to make sure each essay paper is unique and high-quality.
The goal of our college essay writing service is to create both an easy-to-use and professional catalog of paper writers for our consumers. We want every customer to be able to hire an essay writer easily, without any hassle or troubles. Our application gives the ability to access an entire catalog that contains hundreds of writers who write within multiple fields, and we have writers for every specialty. This allows every client to choose the most appropriate author for their assignment.
All of our academic scholars have their profiles. Each profile shows the success rate, a star-rating, and subject specification. Apart from that, we feel it’s important to know your chosen essayist inside out. Thus, they also contain a short biography from the professional writer to enable customers to see what kind of person he or she is. And a list of reviews for the author left by previous clients to give you an insight into customer satisfaction.
Our website is super convenient and easy to use! We work to make sure the experience of our clients is always positive. Buy Cheap College Essays is easy-to-use – with access to customer support who are here to answer any questions or concerns you may have. If you’re in any doubt, keep in mind that our service is legal and legitimate.
For those who are seeking reviews of our service, we have Buy Cheap College Essays reviews page in-app. Take a stroll around the reviews our clients have left us regarding the work and experience they have had. We truly value and take on-board customer feedback. It helps us learn and grow, which widely affects future orders. If you have any concerns, take a look at our reviews page – to find out what clients have said about this paper writing service.
If you are unsatisfied with your essay, do not worry. In that case, our policy states that that customer is entitled to an unlimited amount of free revisions and rewrites within the first 30 days are the completion of the paper. The paper will also be reviewed by another writer with a higher success rate to make sure it is of high quality. We also have a quality assurance team who check the paper for any plagiarism and errors.
If you’re completely unsatisfied with the paper and do not want us to do any more work on it, we offer a money-back guarantee, which is also within the first 30 days of the completion of the order. Meaning, unsatisfied customers also do not need to worry when it comes to a poor quality paper. Though this rarely happens with our service.

Terms And Conditions
Refund Policy
Privacy Policy
Buy Cheap College Essays.com essays are NOT intended to be forwarded as finalized work as it is only strictly meant to be used for research and study purposes.Buy Cheap College Essays does not endorse or condone any type of plagiarism.
College Essay Help
Best Essay Editor
Professional Essay Help
Custom Essay Writing
Buy Essay
Pay For Essay
Rewrite My Essay
Blog